보호도체
어스 도체
어스 도체는 일반적으로 어스 선이라 부른다. 그것은 설치 어스 터미널을 어스 전극 또는 전기 공급회사가 제공하는 어스 터미널과 연결해준다. 그것은 보호 시스템의 필수 연결로서 그것이 완벽하게 되어 있는가를 항상 알아볼 수 있게끔 주의를 기울여야 한다. 알루미늄 도체와 케이블이 어스와 본딩에 쓰이고 있지만 그럴 때는 다른 급속과 접촉하는 부분에서 부식이나 전기분해에 의한 문제들이 생기지 않도록 주의해야 한다.
어스 전극이나 어스터미널 연결이 깨끗하고 영구적으로 완료된 다음에는 “안전 전기연결. 제거하지 마시오”(“Safety Electrical Connection. Do not remove”)라는 레이블을 붙인다({그림 5.17}을 볼 것). 매설한 어스 도체가 절연 피복에 의하여 부식은 방지하고 있으나, 기계적인 손상은 보호하지 못할 경우는 그것이 구리로 되었거나 도금된 철로 되었거나 최소 단면적은 16mm2이 되어야 한다. 만약 어스 도체가 기계적 보호가 안될 뿐만 아니라 부식방지도 안되어 있다면 구리인 경우는 25mm2, 도금된 철인 경우는 50mm2 이상의 단면적을 가져야 한다. 부식 방지가 안된 경우는 기계적 보호가 가능하거나 아니거나 간에 이 최종 규제가 유효하다.
*희생 양극(Sacrificial anode)이란 산화를 방지할 보호해야 할 금속 표면의 음이온 방출을 방지(cathodic protection: 음극 보호)하기 위하여 그 금속보다 더 활성(산화력)이 강한 금속을 표면에 묻히는 것(도금하는 것)을 말한다. --- 역주
주된 어스 터미널이나 바(bar)는 모든 경우의 설치에 있어서 모든 보호 도체와 본딩 도체들을 모아서 연결하는데 제공되어야 한다. 시험의 목적으로만 이 터미널에서 어스 터미널의 연결을 풀 수 있지만 연장(tool)을 사용해서만 가능하게 한다. 이 요구사항은 무자격하거나 잘 알지 못하면서 보호 시스템을 제거(변형)하는 것을 막고자 함이다
보호 도체의 형태
회로 보호 도체란 (cpc라는 약자로 쓰게 되는데) 모든 노출된 도체 부분을 주된 어스 터미널에 연결하는 도체를 말한다, 엄밀하게 말하면, 이것은 어스 도체는 물론 등전위 본딩 도체도 포함한다.
회로 보호 도체는 여러 가지 형태를 취할 수 있는데,
- 피복이 녹색/황색이며, 단면적 10mm2 이상인 분리된 도체
- 다른 도체와 같이 피복된 도체
- 금속 피복 혹은 갑옷 케이블
- 도관이나 트렁크로 둘러싼 도체 케이블의 둘러 싼 금속
- 장비의 케이스처럼 노출된 금속부위
그 밖에 여러 형태를 취할 수 있는데 {그림5.11}에 열거하였다. 주의할 것은 가스나 기름 파이프는 이러한 목적에 사용할 수 없을 것이다. 왜냐하면 앞으로 이러한 파이프는 부도체인 플라스틱으로 바뀔 것이기 때문이다.
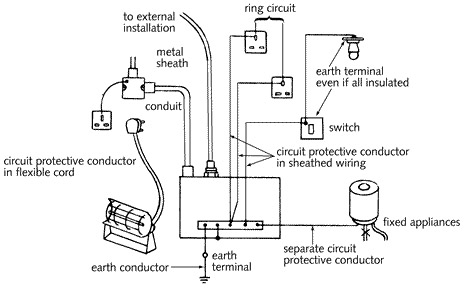
그림 5.11 - 회로 보호 도페의 몇 가지 형태
물론 보호 도체가 설치의 수명이 다할 때까지 그 효과를 유지해야 하는 것이 중요하다. 그래서 보호 목적으로 사용되는 도관의 이음새는 부식이 안되고 또 단단히 연결되어 있도록 많은 주의가 필요하다. 이러한 연결을 명확히 하기 위하여 별도의 (전선으로 된)보호 도체를 도관의 내부에 설치하는 일이 점점 많게 되었다. 물론 이러한 CPC는 플라스틱 보호 도관인 경우는 필수다.
악세서리가, 그것의 CPC가 도관을 사용하는 시스템에 (예를 들어 소켓 아울렛의 수단으로), 연결되는 경우, 시스템의 어스 터미널은 도관 박스의 어스 터미널과 분리된 도체에 의하여 연결 되어야 한다{그림 5.11}. 이 연결은 악세서리가, 심지어 도관과 박스를 조여주는 스크류가 느슨해지거나 손상이나 부식을 당해도, 적정한 연결이 보장되게 하는 것이다.
자유롭게 구부러지는 도관(flexible conduit)을 사용하는 경우는 그것이 낮은 저항을 가질 수는 없으므로 내부에 분리된 보호도체를 같이 배선해야 한다{그림 5.12}
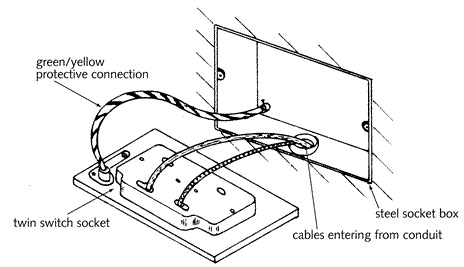
그림 5.12 - 도관 시스템에서 소켓 아울렛을 위한 보호 도체의 연결
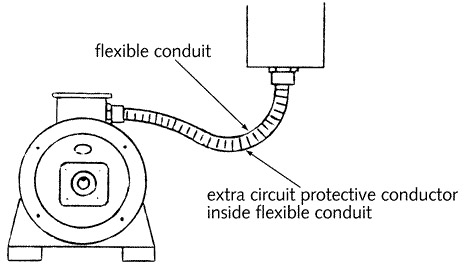
그림 5.12 - 유연성 도관의 분리된 보호도체의 추가
본딩 도체
보호 도체의 목적은 어스폴트의 귀환 경로로서, 폴트 조건상 피할 수 없는 위험한 전위차로 인하여 쇼크가 전해지기 전에, 위험한 전위차를 제거하고자 하는 것이다. 등전위 본딩은 어스된 금속부위(노출된 도체부위)를 다른 금속부위들과 연결하여 위험한 전위차를 없게 하려는 것이다. 이들 본딩 도체의 저항은 충분히 낮아서, 동작 전류가 흘러도 전위차가 50V이내로 되도록 보장해야 한다.
즉, 본딩 도체의 저항값 R이고 과전류보호 동작 전류가 Ia라 하면,
R < 50/Ia 이다.
두 가지 형태의 등전위 본딩 도체 규격이 있다.
1.주된 등전위 본딩 도체
이것은 전기 시스템의 어스 시스템과 가스나 수도와 같은 다른 서비스의 금속부위를 연결하는 것이다. 이것은 건물에 있어서 가스나 수도의 인입부(계량기 바로 지나서)와 가장 가까이에서 서로 본딩해야 한다{그림 5.13}. 전화 통신 케이블의 껍질도 본딩되어야 하겠으나, 그렇게 하기 전에 케이블의 주인(통신회사)에게 승낙을 받아야 할 것이다.
본딩 도체의 최소 사이즈는 전기 공급선의 사이즈와 관련이 있어서 {표 5.6}에 나타냈다.
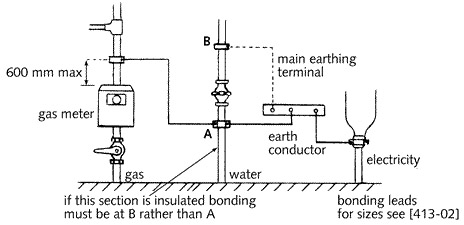
그림 5.13 - 주된 본딩 연결
|
회로 보호 도체 |
보완 본딩 도체 사이즈 (mm2) | |
|
기구적 보호 없음 |
기구적 보호 되어있음 | |
|
1.0 |
4.0 |
2.5 |
|
1.5 |
4.0 |
2.5 |
|
2.5 |
4.0 |
2.5 |
|
4.0 |
4.0 |
2.5 |
|
6.0 |
4.0 |
4.0 |
|
10.0 |
6.0 |
6.0 |
2.보완 본딩 도체
이것은 본질에서 벗어난 부외(extraneous) 도체 부품들, 즉, 전기 설치와 관련이 없지만 쇼크를 일으키는데 기여할 수 있는 것과의 연결이다. 그 목적은 금속제품 사이에서 발생할 수 있는 전위차가 50V를 초과하지 않도록 함에 있다. 이것은 즉, 본딩 도체의 저항이 낮아야 한다는 것이다. {표 5.7}을 참조한다. {그림 5.14}는 본딩해야 하는 목욕실에 있는 몇 가지 부외 도체 부품들을 보여준 것이다.
보완 본딩에서 요구되는 도체의 단면적은 {표5.6}에 나타나 있다. 부외 도체들끼리의 연결은 기계적으로 보호된 경우 2.5mm2, 그렇지 않은 경우는 4mm2의 단면적을 가진 도체로 한다. 만약 회로 보호 도체가 10mm2를 넘는다면 보완 본딩은 적어도 그 절반의 단면적을 가져야 한다. 보완 도체의 단면적이 16mm2 이하에서는 알루미늄 도체를 사용해서는 안 된다. {그림 5.15}에 보완 본딩을 하지 않으면 심각한 쇼크를 일으킬 수 있는 누전될 수 있는 전기 냄비의 살아있는 케이스와 주변의 수도꼭지 사이의 보완 본딩을 보여준다.
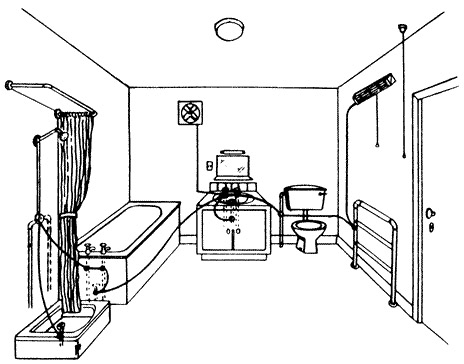
그림 5.14 - 목욕실의 보완 본딩
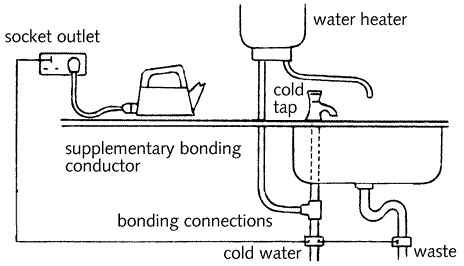
그림 5.15 - 부엌의 보완 본딩 도체
어떤 때는 금속부위가 왜 본딩 돼야만 하는가 하는 의문이 든다. 이에 대한 답은, 살아있는 시스템과 문제의 그 금속 부위가 접촉되어 심각한 쇼크의 위험이 있을 것이므로, 본딩은 언제나 필요한 것이다 라는 것이다. 금속부위와 땅덩어리 사이의 저항이 충분히 낮아서 위험한 쇼크 전류의 통과를 보장하는 것이고, 따라서 금속부위는 본딩이 돼야 한다.
의문은 금속부위에서 주된 어스 터미널에 이르는 저항을 재 봄으로서 판정할 수 있다. 그 저항을 다음 식에 대입하여 사람 몸을 통하여 흐르게 될 최대 전류를 계산할 수 있을 것이다.
Ib = Uo / (Rp + Rx)
여기서 Ib는 몸을 통한 쇼크 전류, Uo는 공급 전압, Rp 는 사람 몸의 저항, Rx는 금속부위에서 주된 어스 터미널까지의 저항이다.
사람 몸의 저항은 대체로 1000Ω으로 취급하지만, 욕실에서 사람이 의문의 그 금속부위를 만질 때는 안전하게 보아 약 200Ω이 된다. 안전한 쇼크 전류 Ib의 값에 대한 쉽고 빠른 규칙이 있는 것은 아니지만 아마 10mA는 좀처럼 치명적이 아닐 것이라 할 수 있다. 사람의 저항(Rp)을 1000Ω으로 보고, 공급전압(Uo)을 240V로 하여, 금속부위의 주된 어스 터미널까지 저항(Rx)를 계산하면 23kΩ이 된다. 만약 안전전류 Ib를 5mA로 하고, 사람 몸의 저항 Rb를 200Ω이라 하면 전압 Uo 240V일 때 어스 저항 Rx는 47.8kΩ 이 된다.
금속부위가 보완 본당이 필요한지 의심스러울 때는 주된 어스 터미널에 이르는 저항을 측정한다. 만약 그 값이 50kΩ이 넘으면 본딩은 필요 없다. 사람이 젖어있지 않을 때는 그 저항이 25kΩ 이상이면 본당 안 해도 된다. 본딩 도체가 그 중요성을 생각하지 못하는 사람에 의하여 제거되는 것을 방지하기 위하여 {그림 5.17}에 보인 것과 같은 레이블을 붙여야 한다.
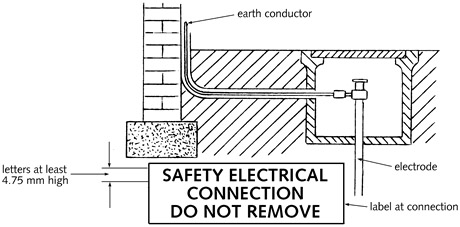
그림5.17 - 제거 방지를 위한 레이블과 어스 도체의 전극 연결
보호 도체 단면적 결정
어스폴트가 생기면 폴트 전류가 흐른다. 만약 이 전류가 충분히 크다면 보호 장치가 빨리 작동할 것이고, 보호도체와 노출된 도체는 위험함 쇼크가 충분히 생길 수 있는 긴 시간을 어스와 연결하여 위험성이 적게 된다. 폴트전류를 결정하는 요인은 공급 전압과 어스폴트 고리 임피던스이다.
어스폴트는 보호도체를 공급 전압과 결과적으로 직렬로 놓게 된다. 어스된 금속부위의 전압(보호도체와 상 도체 사이의 전압)은 이때에는 전기시설이 규격을 제대로 적용하였다 해도 위험스럽게 높아진다. 전기 시설을 사용하는 사람들은 퓨즈나 회로차단기의 능력을 가지고 위험한 결과를 갖기 전에 공급을 차단한다.
기억할 것은 낮은 폴트레벨은 보호장치가 동작하기 전에 긴 시간을 필요로 한다는 것이다. 보호도체의 단면적은 일반적으로 살아있는 도체보다 적은 단면적을 가질 것이므로 폴트가 일어나는 동안에 그것의 저항으로 인하여 열이 더 많이 생긴다, 그러므로 쇼크 전압은 공급전압의 높은 비율을 차지하게 된다.
쇼크 위험이 자장 높은 곳인 소켓 아울렛 회로에서는 {표5.3}에 보인 보호도체의 최대 저항은 쇼크 전압이 50V를 결코 넘지 않게 보장하는 값이다. 만약 관련된 회로가 링(ring)의 형태라 하면 링을 한 바퀴 도는 보호도체의 저항의 1/4이 {표5.3}의 값보다 작아야 한다. 이것은 폴트가 정확하게 링의 중간 점에서 발생할 것이라는 가정에서 나온 것이다. 폴트가 다른 점에서 생길 경우는 유효 저항 값이 링 전체 저항 값 보다 더 적게 되고 그래서 더 안전하게 될 것이다.
표5.7은 어스와 본딩 도체의 사이즈를 계산한다기보다는 선택하게 하는 것이다. 선택에 적용하는 법칙은 다음과 같다. 16mm2까지의 상 도체를 위해서는 보호 도체도 같은 사이즈가 된다. 16에서 35mm2까지의 상 도체를 위해서는 보호 도체는 16mm2 사이즈라야 한다. 35mm2 이상의 상 도체를 위해서는 보호 도체는 적어도 상 도체의 단면적의 절반은 되어야 한다. 분리된 CPC의 최소 단면적은 기구적인 보호가 되어 있다면 2.5mm2, 그렇지 않다면 4mm2이다.
주의할 것은 지역의 전력회사는 설치 초에 최소한의 보호 도체 단면적 16mm2 를 요구하게 된다는 것이다. 그러므로 설치를 설계할 때에는 항상 그들과 상의해야 한다.
|
상 도체 |
어스 도체(매설하지 않은 것 또는 기계적으로 보호된 것) |
PME 공급을 위한 주된 등전위 본딩도체 |
주된 등전위 |
|
4 |
4 |
6 |
10 |
|
6 |
6 |
6 |
10 |
|
10 |
10 |
6 |
10 |
|
16 |
16 |
10 |
10 |
|
25 |
16 |
10 |
10 |
|
35 |
25 |
10 |
10 |
|
50 |
25 |
16 |
16 |
|
70 |
35 |
16 |
25 |
보호 도체 단면적 계산
회로 보호도체의 단면적은 폴트 사고에서 그것에 의하여 가능한 쇼크의 레벨에 관계되기 때문에 매우 중요하다. 안전은 언제나 {표5.7}를 기본으로 사용한 사이즈를 선택한다면 보장이 된다.
그러나 이렇게 하면 계산상으로 용납할 수 있는 것보다 가끔 큰 도체를 사용하게 되기 때문에 다소 비싼 설치가 될 것이다. 예를 들면 절연 피복선으로 1mm2만 큰 도체이면 될 것을 {표 5.7} 의 요구보다 회로보호도체가 적다고 해서 부적격 처리하게 되기 때문이다.
많은 경우에서 CPC 사이즈 계산 값은 {5.4.4.}에서 상세히 보여준 값보다 적은 사이즈이지만 완전히 적합한 것이다. 단면적을 계산하는 공식은 다음과 같다.
S = √(Ia2t) /k -------- ※
여기서 S는 보호도체의 최소 단면적, Ia는 폴트 전류, t는 보호장치의 작동(open) 시간, k는 도체 재질과 절연 그리고 초기 및 최대 절연 온도와 관계되는 비례상수이다.
이 공식은 *단열 방정식(도체에서 생긴 에너지가 열의 형태로 도체에 남아 있는 상태의 방정식)을 활용하는 것이다. *단열 방정식은 다음과 같은 식이다.
t = k2S2 / I2
여기서 t 는 폴트 전류가 도체의 온도를 최대 허용 온도까지 올리는데 걸리는 시간(초)
k 는 케이블의 형태에 의한 비례상수
S 는 도체의 단면적(mm2)
I 는 폴트 전류로서 단락 기대 전류(PSC: prospective short circuit current)
|
절연 재료 |
초기 추정 |
최종 제한 |
k |
|
p.v.c |
70 |
160 |
115 |
|
85°C p.v.c |
85 |
160 |
104 |
|
90°C 온도 세팅 |
90 |
250 |
143 |
|
광산용, 노출되었거나 p.v.c. 덮힘. |
70 |
160 |
115 |
|
노출되지 않은 광산용 |
105 |
250 |
135 |
단면적을 계산하는 공식※으로 세 가지 정보, 즉, Ia, t, k 를 얻을 수 있다.
1) Ia 구하기
Ia = Uo / Zs 단, Uo는 공급 전압 (240V), Zs는 폴트가 제로 임피던스(이른바 쇼트)로 가정할 때의 어스폴트 임피던스 설계단계에서는 어스 루프 임피던스를 측정할 수 없기 때문에 외부 설치 임피던스에 관련 회로의 제일 먼 거리까지의 도체 저항을 더하여 계산해야 한다. 이 기법은 {5.3.6}에서 사용하였다. 즉 Zs = Ze + R1 + R2, R1과 R2는 각각 상과 보호 도체의 저항[{표 5.5}에 의함]이다.
2) t 구하기
앞에서 이미 구한 Ia 값을 사용하여 {그림 3.13}부터 {그림 3.19}까지의 시간 전류 특성에 의하여 보호장치 동작시간 t를 구할 수 있다. 예를 들어 보호 장치가 20A의 타입 1 소형 회로 차단기이고 폴트 전류가 1000A인 경우 {그림 3.16}에서 차단 시간 t가 0.01초인 것으로 읽게 된다. (여기서 흥미로운 것은 폴트 전류가 80A라 하면 t는 0.04부터 20초까지 어느 것이든 될 수 있으니 요구하는 개방시간을 적용하지 못하게 될 것이다.)
3) k 구하기
k는 우리가 계산해 낼 수는 없고 적당한 표로부터 얻어야 한다. 몇 가지 대표적인 보호도체에 대한 k 값을 {표 5.8}에서 얻을 수 있다.
|
보호도체의 성격 |
초기 온도 |
최종 온도 |
도체 재질 |
K |
|
묶여지지 않은 p.v.c. 절연선 |
30 |
160 |
동(구리) |
143 |
|
- |
30 |
160 |
알루미늄 |
95 |
|
- |
30 |
160 |
철(쇠) |
52 |
|
- | ||||
|
케이블 안에 또는 묶여진 |
70 |
160 |
동(구리) |
115 |
|
- |
70 |
160 |
알루미늄 |
76 |
|
- | ||||
|
철제 도관 |
50 |
160 |
철(쇠) |
47 |
|
- | ||||
|
벗겨진 도체 |
30 |
200 |
동(구리) |
159 |
|
- |
30 |
200 |
알루미늄 |
105 |
|
- |
30 |
200 |
철(쇠) |
58 |
예제 5.2
240V 단상 전원 공급에서 30A를 소모하는 부하가 있고 이것이 BS88에 의한 32A HBC 퓨즈로 보호된다. 배선은 도관 안에 PVC 절연한 단심의 4mm2로 배선 거리는 18m 이다. 외부에서 설치에 이르는 어스폴트 고리 임피던스는 0.7Ω이다. PVC 절연 피복선으로 적당한 보호도체의 단면적을 계산한다.
풀이
이것은 문제를 풀기 전에 답에 대한 가정을 하는 것이 필요한 경우의 하나이다. 보호 도체가 2.5mm2이면 적절할 것이라고 가정하고 회로의 끝에 이르는 절연의 기원에서 상과 보호도체의 복합 저항을 계산하자. {표 5.5}에서 2.5mm2 케이블은 7.4mΩ/m이고 4mm2은 4.6mΩ/m인 저항률을 가진다는 것을 알 수 있다. 이 두 가지 값에 1.2를 곱하여 폴트 전류가 흐를 때의 온도 상승에 대비한다. 그리하여
R1 + R2 = [{(7.4 + 4.6) x 18}/1000] x 1.2 = 0.26 (Ω) 가 된다.
이 도체의 저항 값은 외부 고리 임피던스 값 Ze 와 합하여 전 고리 임피던스 Zs는
Zs = Ze + R1 + R2 = 0.7 + 0.26 = 0.96 (Ω) 이다.
이제 폴트 전류를 계산해 보면
Ia = Uo/Zs = 240/0.96 = 250 (A) 이다.
다음 전류 250A에 대한 위의 퓨즈 동작 시간을 알아본다. {그림 3.15}의 시간/전류 특성에 의하여 0.2초에 퓨즈가 단락 됨을 알 수 있다. 끝으로 상수 k 값을 알아보면 {표 5.8}에서 도관 안에 다른 것들과 묶여 있으므로 115라는 것을 알 수 있다. 이제 Ia, t, k 값에 의하여 도체의 단면적을 계산하면
S = (Ia2t) / k = √(2502 x 0.02) / 115 = 0.97 (mm2) 가 된다.
이 결과 값은 1mm2이 보호도체로 적합하다는 것인데, 이 모든 계산이 단면적 2.5mm2을 가정하여 출발한 것이므로 어긋난 계산이 된다. 따라서 가정을 바꾸어 1.5mm2로 단면적을 정하고 계산의 전 과정을 다시 해 본다.
다시 계산해 본 결과 보호도체의 저항 값은 저항률이 {표 5.5}에서 18.1 mΩ/m이고, 4mm2 상 도체와 같이 R1 + R2 저항 값에 온도 감안하여 도체 저항은 0.491Ω이 된다. 외부 고리 임피던스를 더한 전 어스폴트 고리 임피던스는 1.191Ω이 되어 전원전압 240V에 대한 폴트 전류는 202A로 계산된다. {그림 3.15}에 의하여 보호 동작 시간은 0.6초가 되고 k 값은 변화 없이 115이므로 보호도체의 단면적은
S = √(la2t) / k = √(2022 x 0.6) / 115 = 1.36 (mm2) 이다.
그래서 보호도체의 단면적이 1.5mm2 인 것이 적합하고 처음 출발한 가정과 부합된다. 주의할 것은 만약 사이즈를 계산으로 하지 않는 표에 의한 선정이면 4mm2가 되어 사이즈는 두 단계 큰 것이 된다는 것이다. 여기서 조심할 것은 단락 시간이 계산으로 하면 0.6초여서 소켓 아울렛의 요구 사항인 0.4초보다 길어진다는 것이다.
예제 5.3
240V, 30A의 링회로 소켓 아울렛이 45m 길이로 2.5mm2의 얇은 두 가닥 붙인 PVC 절연피복선으로 배선하고 보호도체(CPC)는 1.5mm2의 단면적을 가진 것으로 같이 배선되어 있다. 회로는 BS 3036에 따른 반 복개(semi-enclosed) 퓨즈로 보호하며 어스폴트 고리 임피던스는 외부에서 설치까지 0.3Ω이다. 피복선으로 단면적 1.5mm2인 CPC가 적합함을 입증한다.
풀이
먼저 {표 5,5}를 써서 상과 CPC의 도체의 저항 값을 찾는다. 이들은 저항률이 각각 7.4 그리고 12.1 mΩ/m 이므로 45m 길이로는 온도 상승을 감안할 때 링 전체 저항은
R1 + R2 = {(7.4 + 12.1) X 45 /1000} X 1.2 = 1.05 (Ω) 이다.
링 회로에서 어스폴트 임피던스는
Zs = Ze + (R1 + R2)/4 = 0.3 + 0.263 = 0.263 (Ω) 이다.
따라서 어스폴트 전류는
Ia = Uo/Zs = 240/0.563 = 426 (A) 이다.
{그림 3.13}에서 이 전류에 대한 시간/전류 특성을 이용하여 시간을 읽으면 보호동작 시간은 0.10초가 된다. 또 {표 5.4}에서 k가 115이므로 CPC의 단면적은
S = √(Ia2t) / k = 4262 X 0.1 / 115 = 1.17 (mm2) 이다.
이 값은 주어진 1.5mm2보다 적으므로 1.5mm2은 적합하다.
예제 5.4
240V 단상회로가 PVC 절연 단심 코어 케이블로 플라스틱 도관 안에 배선되어 있다. 회로 길이는 45m이고 살아있는 도체는 단면적이 16mm2이다. 회로는 고정된 장치에 공급하며, BS 88에 의한 63A HBC 퓨즈에 의하여 보호한다. 외부에서 설치까지 어스폴트 임피던스 고리 임피던스는 0.58Ω이다. 회로 보호도체의 적정한 사이즈를 계산한다.
풀이
이 문제에서 주어진 정보로는 문제를 푸는데 특별한 접근 방법이 필요하다.
고정된 도체를 위한 최대 단락 시간은 5초로 알고 있다. {그림 3.15}에서 63A 퓨즈의 시간/전류 특성에서 단락할 수 있는 최소 전류 값은 280A이다. 따라서 어스폴트 고리 임피던스는
Zs = Uo/Ia = 240/280 (Ω) 이다.
또 어스폴트 고리 임피던스에서 외부 임피던스를 빼주면 R1 + R2는
R1 + R2 = Zs – Ze = 0.857 – 0.58 = 0.277 (Ω)이 된다.
배선길이가 45m이므로 단위 길이당 저항률을 내보면 온도 상승을 감안할 때
0.277 X 100/(45 X 1.2) = 5.13 (mΩ/m) 가 된다.
{표 5.5}에 의하면 16mm2 구리도체는 저항률이 1.15 mΩ/m이고, 반면에 10mm2은 1.83mΩ/m이고 6mm2은 3.08mΩ/m이다. 상 도체(16mm2)의 저항률에 어떤 도체의 저항률을 더하여 위에서 계산한 5.13mΩ/m에 근접할 수 있는가를 보면 3.08mΩ/m가 적합하다. 따라서 보호도체의 단면적은 6mm2가 적합하다. 이것이 적합한가를 검산해보려고 하면 단열 방정식을 점검해야 한다. 단면적 6mm2의 보호도체와 단면적 16mm2의 상 도체에 의한 R1 + R2를 계산하면
R1 + R2 = {(1.15 + 3.08)/1000} X 1.2 X 45 = 0.228 (Ω)이다
어스폴트 고리 임피던스는
Zs = Ze + R1 + R2 = 0.58 + 0.228 = 0.808 (Ω)이다.
폴트 전류는
Ia = Uo/Zs = 240/0.808 = 297 (A)이다.
{그림 3.15}에서 63A 퓨즈에서 297A는 단락시간이 3.8초가 되고, {표 5.8}에서 k 값이 115이므로 단면적 S는
S = √(Ia2t) / k = √(2972 x 3.8) / 115 = 5.03 (mm2)가 된다.
5.03은 6보다 적으므로, 단면적이 6mm2 인 보호도체는 충분히 커서 요구 조건을 만족하게 된다.
어스가 안된 금속물체
노출된 도체 부품이 독립하여 있거나, 비 전도성 물질로 둘러싸여 있거나, 사람 몸에 의하여 접촉될 수 있는 면적이 제한되어 있다면, 그들을 어스하지 않아도 된다. 보기로 사람이 닿을 수 없는 높은 위치에 걸쳐 있는 고상선, 콘크리트로 둘러싸인 철 보강 막대, 케이블 고리, 명판, 고정 스크류 등이 있다. 특수 기술자나 선별된 사람만 접근할 수 있는 장소 그리고 경고나 주의간판이 있어서 무자격자는 근접할 수 없거나 잠겨있는 장소 등과 어스하는 것이 장애를 받는다는 법률규제가 있어 직접 접촉이 안 되는 장소에 있는 것도 해당된다.
'[참고 자료] > 전기, 전력 일반' 카테고리의 다른 글
| 어스 (0) | 2010.09.09 |
|---|---|
| 어스 시스템 (0) | 2010.09.09 |
| 교류회로의 기초이론 (0) | 2010.02.20 |
| 배전자동화 기술개발 현황과 전망 (0) | 2009.09.29 |
| 국내 전력설비 예방진단 기술 적용 본격화 (0) | 2009.08.24 |